Los sólidos platónicos, denominados así en honor al filósofo griego Platón, son figuras geométricas tridimensionales que han fascinado a matemáticos y científicos desde la antigüedad. Estas formas no solo son estéticamente perfectas, sino que también juegan un papel fundamental en diversas ramas de las matemáticas y la ciencia. Su estudio revela propiedades geométricas y simetrías que han sido exploradas y admiradas durante siglos.
Definición y características
Un sólido platónico es un poliedro convexo cuyos rostros son polígonos regulares idénticos, es decir, todas las caras del sólido tienen la misma forma y tamaño, y los ángulos de los polígonos se encuentran en los vértices del sólido en la misma disposición. Además, cada arista es compartida por dos caras idénticas, y los ángulos entre las aristas son iguales en todos los vértices.
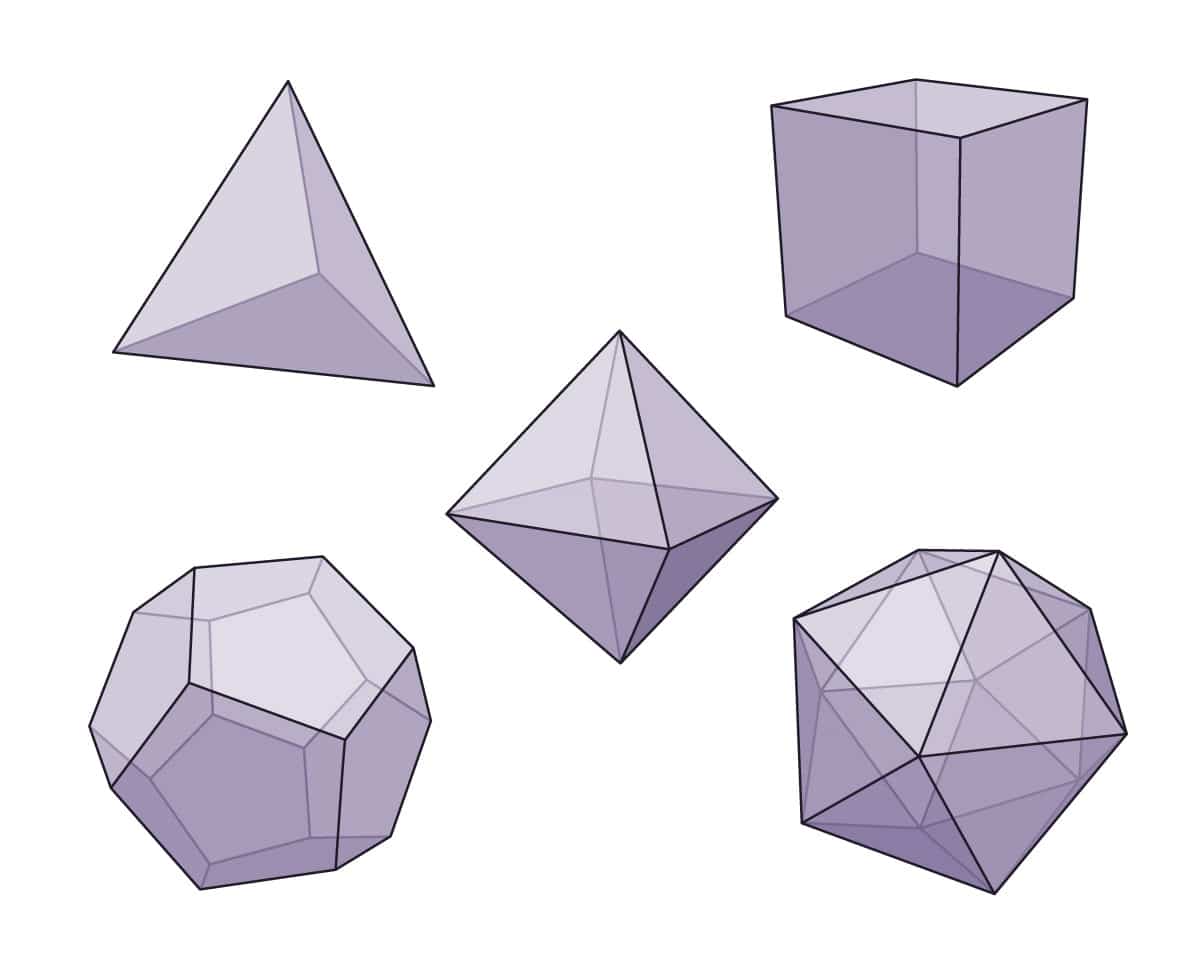
Existen solo cinco sólidos platónicos, que se clasifican de la siguiente manera:
- Tetraedro: Este sólido tiene 4 caras, todas triángulos equiláteros. Cada vértice del tetraedro está unido por tres aristas, y cada ángulo interno de los triángulos equiláteros es de 60 grados.
- Cubo (o Hexaedro Regular): El cubo posee 6 caras, todas cuadrados. Cada vértice del cubo está unido por cuatro aristas, y cada ángulo interno de los cuadrados es de 90 grados.
- Octaedro: Este poliedro tiene 8 caras, todas triángulos equiláteros. Cada vértice está unido por cuatro aristas, similar al cubo pero con una estructura completamente diferente.
- Dodecaedro: Compuesto por 12 caras, todas pentágonos regulares, el dodecaedro tiene cinco caras conectadas en cada vértice.
- Icosaedro: El icosaedro tiene 20 caras, todas triángulos equiláteros. Cada vértice está conectado por cinco aristas.
Propiedades matemáticas
Cada sólido platónico tiene una serie de propiedades matemáticas distintivas:
- Número de Caras, Vértices y Aristas: La relación entre el número de caras FFF, vértices VVV, y aristas EEE en un sólido platónico sigue la fórmula de Euler para poliedros convexos: V−E+F=2V – E + F = 2V−E+F=2. Esta fórmula es fundamental en la teoría de poliedros y proporciona una conexión matemática profunda entre estas características.
- Simetría: Los sólidos platónicos son altamente simétricos. Cada uno de ellos presenta simetría rotacional y reflexiónal, lo que significa que puede ser rotado o reflejado de varias maneras sin cambiar su apariencia. Esta simetría se describe mediante grupos de simetría específicos que capturan todas las transformaciones que mantienen la forma del sólido.
Aplicaciones y relevancia
Los sólidos platónicos no solo tienen un valor estético y teórico, sino que también encuentran aplicaciones en varias áreas:
- Cristalografía y Química: En química, los sólidos platónicos se relacionan con la estructura de ciertos compuestos moleculares. Por ejemplo, las moléculas de metano y el fullerene (C60) adoptan formas que se pueden describir mediante sólidos platónicos.
- Arquitectura y Arte: La simetría y la belleza geométrica de los sólidos platónicos han inspirado a arquitectos y artistas a lo largo de la historia. Su estudio también es esencial en la teoría del diseño y en la construcción de estructuras complejas.
- Matemáticas y Física: En matemáticas, los sólidos platónicos son objetos fundamentales en la geometría y la teoría de grupos. En física, la simetría de estos sólidos ayuda a entender los principios fundamentales de la física de partículas y las estructuras cristalinas.
En resumen, los sólidos platónicos representan un campo de estudio fascinante que combina la belleza estética con la profundidad matemática. Su unicidad y simetría los han convertido en un tema central en diversas disciplinas, demostrando que la geometría no solo describe el mundo que nos rodea, sino que también ofrece una ventana hacia la comprensión más profunda de la naturaleza.











