La Inteligencia Artificial (IA) se ha convertido en una de las tecnologías más revolucionarias de nuestro tiempo. Sin embargo, detrás de esta aparentemente «mágica» capacidad de las máquinas para aprender y tomar decisiones, se encuentra una base sólida de matemáticas que se ha desarrollado durante siglos. Para comprender cómo funciona la IA moderna, es esencial reconocer el papel fundamental de disciplinas matemáticas como el cálculo, la probabilidad, el álgebra lineal y muchas otras, que han sido la clave para su evolución.
Cálculo y Optimización: De Newton a las Redes Neuronales
El desarrollo del cálculo en los siglos XVII y XVIII por matemáticos como Isaac Newton y Gottfried Wilhelm Leibniz no solo transformó la física, sino que también sentó las bases para muchos de los algoritmos que hoy son esenciales en la IA. La optimización, que se basa en el cálculo de derivadas y el ajuste de parámetros, es crucial para el entrenamiento de redes neuronales. Estos principios, conocidos como retropropagación (backpropagation), son esenciales para el aprendizaje de máquinas y el ajuste de los modelos, sin los cuales no existirían los avances actuales en la IA.
En el ámbito educativo, el conocimiento de estos principios matemáticos es crucial para los estudiantes que buscan comprender cómo los algoritmos optimizan su rendimiento y cómo las máquinas aprenden de los datos.
Probabilidad y Estadísticas: Gestionando la Incertidumbre
La probabilidad y las estadísticas, campos fundamentales desarrollados por matemáticos como Thomas Bayes y Carl Friedrich Gauss, permiten que la IA maneje la incertidumbre y tome decisiones en condiciones de información incompleta. Estos campos matemáticos son cruciales para el diseño de sistemas de IA que predicen comportamientos, clasifican datos o realizan recomendaciones. El uso de la probabilidad en la IA permite modelar situaciones de incertidumbre, algo esencial en los sistemas de IA generativa y en las decisiones automatizadas.
En un contexto educativo, la estadística es una herramienta poderosa para enseñar a los estudiantes a interpretar datos, realizar predicciones y tomar decisiones basadas en la probabilidad, habilidades que son cada vez más valiosas en el mundo moderno.
Álgebra Lineal: El Lenguaje de las Redes Neuronales
El álgebra lineal es uno de los pilares de la IA moderna, especialmente en el contexto del aprendizaje profundo. Vectores, matrices y tensores son estructuras matemáticas que permiten a los modelos de IA procesar grandes volúmenes de datos de manera eficiente. Las redes neuronales, como las utilizadas en GPT o DALL·E, operan mediante transformaciones lineales de estos datos, lo que permite que los modelos aprendan a partir de ellos.
El álgebra lineal es esencial en la educación matemática moderna, ya que forma la base para comprender cómo las máquinas «piensan» y cómo se procesan los datos. Los estudiantes que dominan el álgebra lineal están mejor preparados para entender el funcionamiento interno de los algoritmos de IA.
Teoría de la Información: La Base de la Compresión y el Procesamiento de Datos
Claude Shannon, con su teoría de la información, introdujo conceptos fundamentales como la entropía, que mide la cantidad de información y la incertidumbre en los sistemas de comunicación. La teoría de la información es vital en el campo de la IA moderna, ya que permite entender cómo se procesan, almacenan y comunican los datos dentro de las redes neuronales. Gracias a esta teoría, podemos optimizar la eficiencia de las redes de IA, mejorar su capacidad de respuesta y generar resultados más precisos.
En la educación, esta teoría puede enseñar a los estudiantes a comprender cómo funciona la comunicación de datos y cómo se puede optimizar el uso de la información en diversas áreas, desde la compresión de archivos hasta las redes sociales.
Lógica y Matemáticas Discretas: La Estructura de los Algoritmos
Las matemáticas discretas y la lógica matemática son fundamentales para el diseño de algoritmos. La lógica permite estructurar el razonamiento y desarrollar procesos de toma de decisiones que son la base de muchos algoritmos de IA, como los árboles de decisión o la generación de código. La lógica matemática también es la base de la IA simbólica, en la que las máquinas razonan y manipulan símbolos como lo haría un ser humano.
Para los estudiantes de matemáticas y ciencias de la computación, el estudio de la lógica y las matemáticas discretas es esencial para entender cómo funcionan los algoritmos y cómo se estructuran los sistemas de IA.
Teoría de Conjuntos: Entendiendo los Datos
La teoría de conjuntos, desarrollada por Georg Cantor, es fundamental para la organización y clasificación de datos en IA. Permite entender cómo los datos se agrupan, se etiquetan y se combinan, facilitando el trabajo con grandes volúmenes de información. La teoría de conjuntos es la base para el modelado de datos y la estructura de las bases de datos que alimentan los sistemas de IA.
En el aula, la teoría de conjuntos se utiliza para enseñar a los estudiantes cómo organizar la información y cómo los conjuntos y las relaciones entre ellos permiten resolver problemas complejos.
Conclusión: La Matemática como Pilar de la IA Moderna
La Inteligencia Artificial moderna no es una tecnología que aparece de la nada, sino el resultado de siglos de avances matemáticos que, finalmente, han sido escalados gracias al poder de las computadoras y los datos. Cálculo, probabilidad, álgebra lineal, teoría de la información y muchas otras disciplinas matemáticas han sido fundamentales para la creación de la IA tal como la conocemos hoy.
Para los estudiantes, entender los fundamentos matemáticos detrás de la IA no solo es importante para comprender cómo funcionan estas tecnologías, sino también para desarrollar las habilidades necesarias para ser parte de la próxima generación de innovadores en este campo. La IA es un reflejo de la belleza de las matemáticas aplicadas a gran escala, y su estudio puede inspirar a futuros científicos, ingenieros y educadores a seguir explorando su potencial.
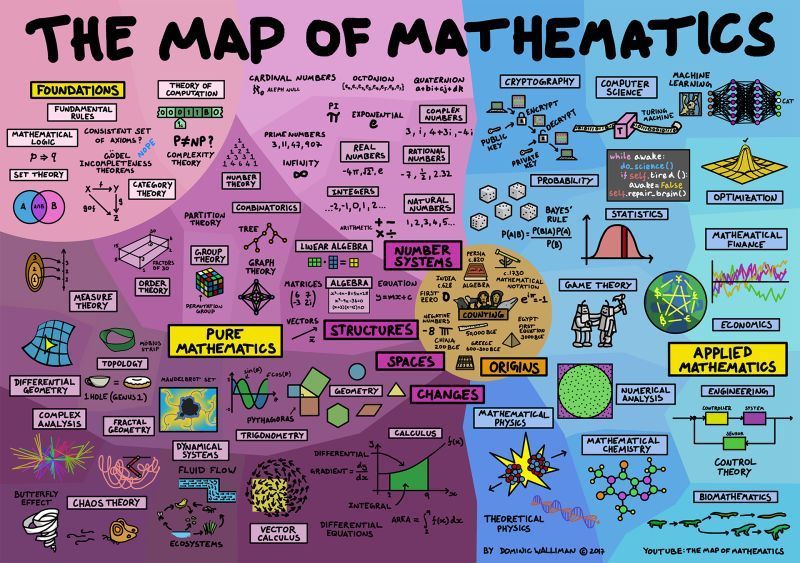
Fuente: Noticias Inteligencia artficial











