¿Alguna vez te has preguntado cómo se crean esos laberintos complejos que aparecen en los libros de pasatiempos? Crear un laberinto a mano es más difícil de lo que parece: si dibujas un solo camino largo, resulta demasiado fácil de resolver; si haces muchos caminos pequeños, terminas con áreas desconectadas. Sin embargo, existe un método matemático elegante que genera laberintos perfectos de forma automática: el Algoritmo de Wilson.
¿Qué hace especial al Algoritmo de Wilson?
Este algoritmo, desarrollado por el matemático David Bruce Wilson en 1996, tiene una propiedad extraordinaria: genera laberintos verdaderamente aleatorios. Esto significa que cada posible configuración de laberinto de un tamaño determinado tiene exactamente la misma probabilidad de ser creada. No hay sesgos, no hay patrones predecibles: pura aleatoriedad matemática.
¿Cómo funciona?
El proceso es sorprendentemente simple de entender, aunque su elegancia matemática es profunda:
Paso 1: Preparación inicial
Imagina una cuadrícula de puntos negros. Selecciona uno al azar y coloréalo de blanco. Este será tu punto de partida, la «semilla» de tu laberinto.
Paso 2: Caminata aleatoria con borrado de bucles
Ahora viene la parte interesante. Elige otro punto negro al azar y coloréalo de blanco. Desde este punto, comienza a caminar en direcciones aleatorias (arriba, abajo, izquierda o derecha), coloreando cada nuevo punto de blanco y dibujando líneas entre ellos.
Aquí está el truco: si accidentalmente caminas de vuelta hacia tu propio camino, creando un bucle, debes deshacerlo. Retrocede hasta el punto donde te intersectaste contigo mismo, vuelve negros todos los puntos por los que pasas al retroceder, borra las líneas, y continúa desde ahí en una nueva dirección aleatoria.
Paso 3: Conexión con el laberinto existente
Continúa tu caminata aleatoria hasta que alcances cualquier punto blanco que ya forme parte del laberinto establecido. Cuando esto ocurra, tu nuevo camino se integra permanentemente al laberinto. Ahora selecciona otro punto negro y repite el proceso.
Paso 4: Completar el laberinto
Sigue agregando nuevos caminos hasta que todos los puntos de la cuadrícula sean blancos. ¡Felicidades! Has creado un laberinto matemáticamente perfecto.
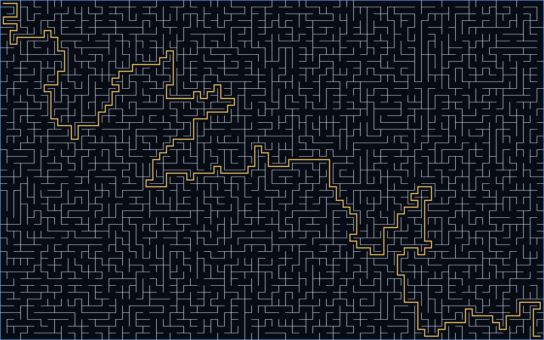
¿Por qué funciona este método?
El Algoritmo de Wilson pertenece a una familia de métodos llamados «caminatas aleatorias con borrado de bucles» (loop-erased random walks). El borrado de bucles es crucial: garantiza que el laberinto resultante sea un «árbol de expansión» perfecto, es decir, una estructura donde existe exactamente un camino único entre cualquier par de puntos, sin ciclos ni áreas aisladas.
La belleza matemática del algoritmo radica en que produce una distribución uniforme sobre todos los posibles árboles de expansión de la cuadrícula, lo que significa que cada laberinto válido tiene la misma probabilidad de aparecer.
Aplicaciones más allá de los pasatiempos
Aunque parece un simple generador de entretenimiento, el Algoritmo de Wilson tiene aplicaciones en:
- Simulaciones físicas: modelos de percolación y procesos de difusión
- Ciencias de la computación: diseño de redes y algoritmos de enrutamiento
- Diseño de videojuegos: generación procedural de mazmorras y niveles
- Investigación matemática: estudio de estructuras aleatorias y procesos estocásticos
Una ventana a la aleatoriedad
El Algoritmo de Wilson es un ejemplo perfecto de cómo las matemáticas pueden tomar algo aparentemente caótico —la aleatoriedad— y canalizarlo para crear estructuras complejas pero perfectamente organizadas. La próxima vez que resuelvas un laberinto en un libro de pasatiempos, recuerda: detrás de esos caminos sinuosos podría estar la elegancia de una caminata aleatoria con borrado de bucles.
¿Te animas a implementarlo? Con solo unas pocas líneas de código y un generador de números aleatorios, puedes crear laberintos infinitamente variados, todos garantizados como únicos y perfectamente resolubles.
Idea sacada del artículo de Cruz Dogar y Carrero